【HDU题解】杭电 Oj 1006 Tick and Tick 个人题解
杭电 oj 1006 Tick and Tick 个人题解
首先贴上官网原题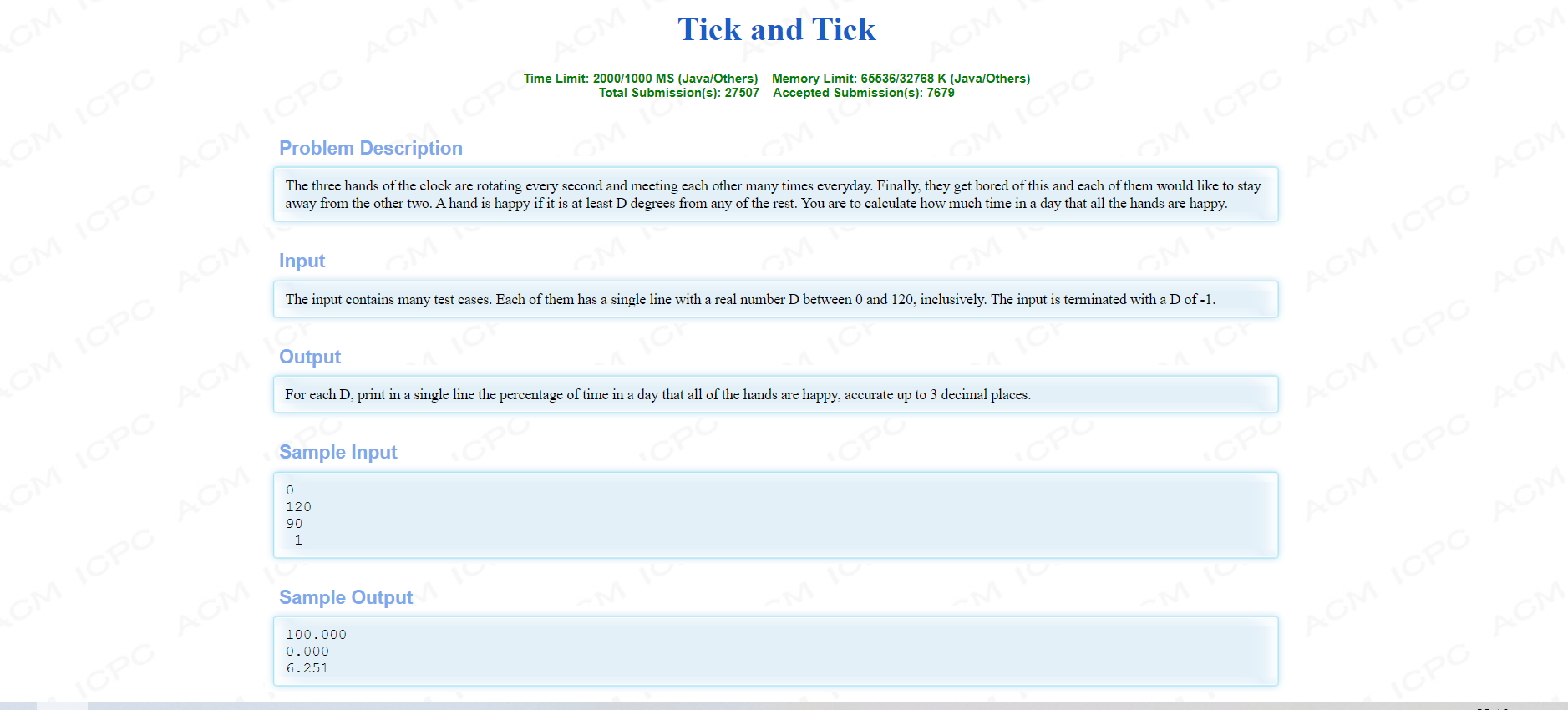
刚开始看到这道题觉得又是一道水题,后面仔细看了一下题目后才知道这道题更加考数学,确实让我纠结了很久。以下是我的一些思路:
思路一:暴力模拟法
可能一般人都会用秒数来模拟时钟,然后根据秒数来确定时针和分针的位置,然后累加时间,这里可以用1s,0.1s,0.01s,甚至是0.001s来作为单位时间模拟,但其实有两大缺点:
1. 单位时间小,要模拟的次数多。
2. 精度不够,要保留小数点后3位。
我用的不是秒数模拟,而是用秒针所走过的度数来模拟,这样可以省去时间与度数的转换。
需要知道的是:秒针的速度=60×分针的速度=720×时针的速度
这里先贴上我写的代码(作为第一种思路提交的,oj上失败了):
1 | |
这里其实有很多细节处理过程,
如:3个if的写法,举其中一例,abs(miao-fen)>=n,是判断miao和fen的度数之差,这里用abs是因为fen的度数有可能超过miao(相对与起始位置)。还有就是后面的(miao-fen+360)>=n和fen-miao+360是用来算另一个夹角的。
然后这个0.45也是调试过好几遍,刚开始用的是0.01,运行后发现运行时间太长了,就把它改大了一些,变成1,虽然测试样例对了,但是提交上去的时候就错了(精度不够)。
贴上提交的图: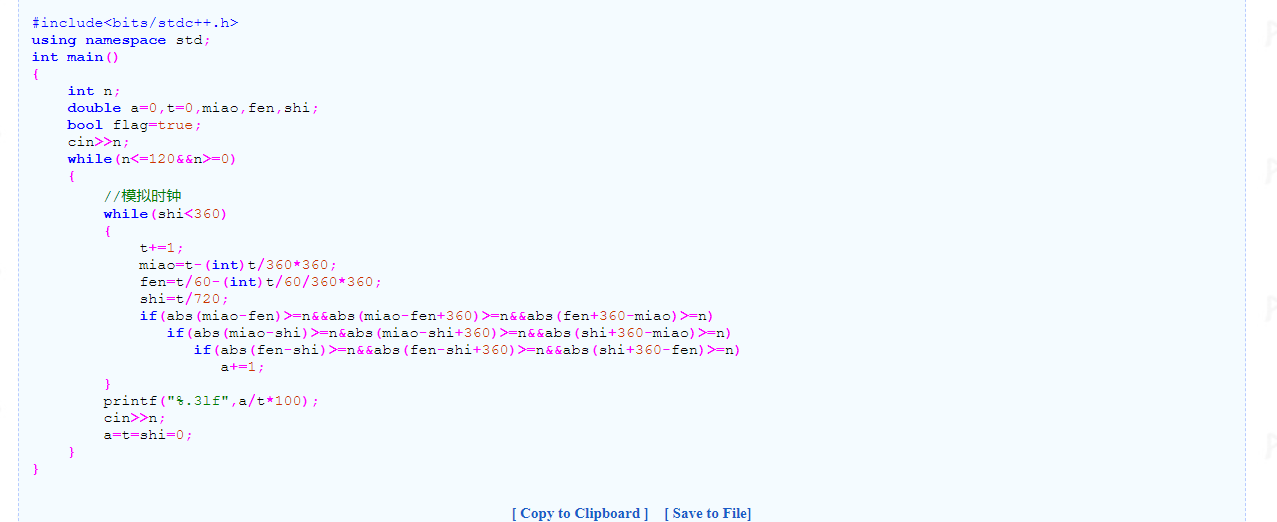

这里可以看到答案错误,而且运行时间还不小。
所以我尝试着用时间来换精度。
结果如图所示: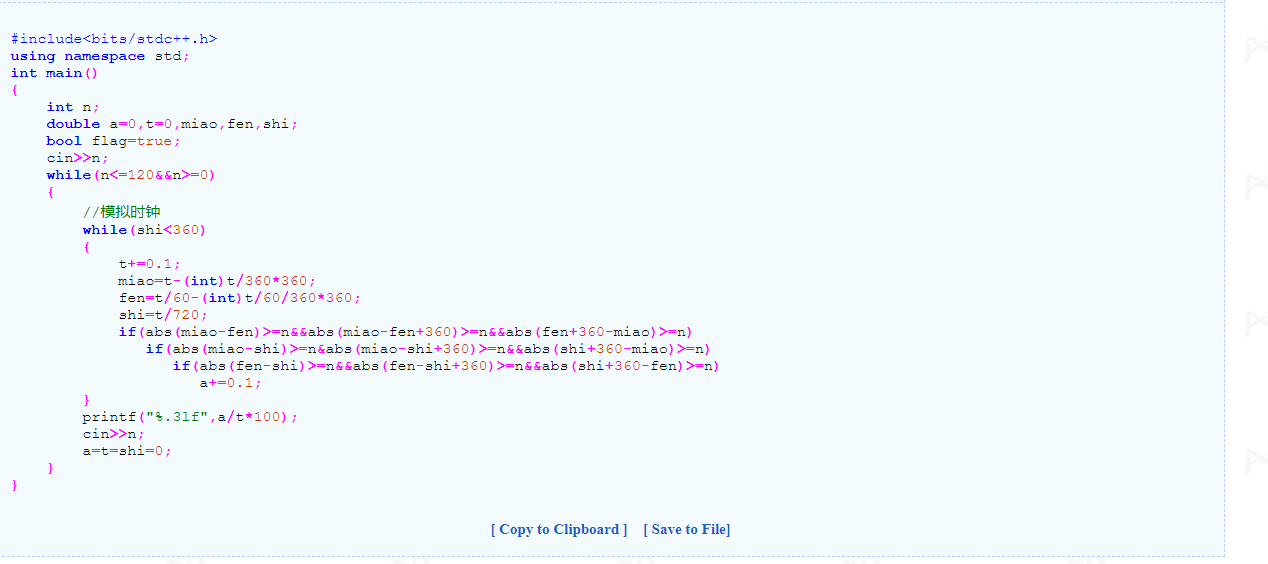

然后尝试着调大一些,调成0.5:
在调小一些(心累),0.45:
事实证明:没有好的算法oj不认!
所以我就开始百度,发现很多其他博主用的是解方程的形式, 但也都是代码一贴,看不懂,或者太长了不想看,本来想着要放弃,但是后来想想不会的题目不去做永远不会,还不如再试试。
今天费了整天,终于死磕出来,也就是思路2。
思路2:解方程,算符合条件的两两之间的区间,最后取交集,合并区间。
闲谈:
先说说我的整个挣扎的过程(不想看的可以直接跳过,博主个人的废话):
开始,我想的是用做数学题的想法,就是先让分针和时针先产生一个n的夹角,算出此时的时间,然后再在此基础之上去确定秒针的位置,这里贴一下我半途而废的代码:
1 | |
但后来才发现不对,t3和t4那个在前面,那个后面呢?t3和t4还要去公共部分,可能会与上一个t3或者上一个t4 时间有重叠等等…….
所以,我决定用计算机特性:能够存储大量数据,来解决所有头疼的问题
正题:
其实回过头来看这道题会发现,无非他让我们做的不就是算出所有满足条件的时间区间,然后相加,最后计算占总时间的比例.
因为一天24小时前12个小时和后12个小时情况相同,所以就用12个小时为总时间.
首先,对于这道题总的框架应该是先计算两两直接满足条件的区间(你也不可能一次性把三个条件全满足的区间算出来)
所以应当是算时针和秒针的区间,时针和分针的区间,以及分针和时针的区间,最后取交集.
先贴上代码再说明:
1 | |

1.
int型:
n 用来存储输入数据
s1 用来存储ms数组的元素个数(预计有1440,保险起见用2000个)
s2 存储fs数组的元素个数(预计24个,用30)
s3 存储fm数组的元素个数(预计1440个,用2000)
s4 存储h1数组的元素个数(预计1440个,用2000)
2.
double数组:
ms数组存的是秒针和时针满足条件的区间(ms是秒时的缩写)
以此类推
h1数组用来存第一次合并的区间(两两合并要2次,本来要有2个数组来存合并区间,但是我是先把fs和fm合并的,所以第二次合并的时候fm数组没用,可以空出来当最终的区间数组,另外主要是fs数组的值很少,先合并fs数组可以少循环几次)
double ans用来存储开心时间.
3.(最核心的部分)
如何算即如何解方程?
其实很简单,我们先以n=90°,秒针和时针为例,我这里用的是度数列的方程,即设秒针走过的度数为x,则第一次满足条件时:
x-x/720=90
那秒针再超过时针一圈呢?
x-x/720=90+360
再来一圈呢?
x-x/720=90+360×2
…
x-x/720=90+360×i
那么解得x=(90+360×i)×720/719.
其实还有一种情况:
还是时针和秒针
当秒针超过时针并去追时针时,第一次满足条件时有:
x/720+360-x=90
同理i圈后:
x/720+360×i-x=90
解得x=(360×i-90)×720/719.
那么可以以此类推秒针和分针,分针和时针的情况.
最后再两两合并,累加时间ans.然后输出比例后记得重置数据,以便下一次的运算.
==
(PS:评论支持一下博主,深夜12:30了,有点困了~ )
附上我的草稿(乱的一)
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!